Here is a direct link to Snap!

To play with Snap! you can just click on the play button on some of the images, like the one above. If you have any problems with it loading, visit Snap! directly in a new browser tab (On that page, click "Run Snap! now"). Another possible solution, if your browser is not Chrome, is to give Chrome a try.

The "Have I Lied?" Game

Today, we're going to play a game called "Have I Lied?". I will ask you "Have I Lied if I say ..." and then make a statement. Your job is to tell me if my statement is true or false.

Have I lied if I say "All birds fly"?

Answer: true (because the statement is a lie/false).... Flightless bird species like penguins do not fly.

Notice the game is a little tricky! When the expressed fact is a lie, then we have to answer true ("yes, you have lied!"). When the given fact is a truth, then we have to reply false ("no, you have not lied!").

Have I lied if I say "Some pizzas are vegetarian"?

Answer: false (because the statement is true)....

Have I lied if I say "All birds fly OR some pizzas are vegetarian"?

Answer: false (because although the first fact is false, the second one is true, and because I said "or" the whole statement becomes a truth)....

Propositional Logic

The above statement actually combined two statements with "or" , to make one larger statement.

This is called the Logical OR or sometimes a Disjunction. In the study of Propositional Logic (which is what we are doing) the symbol ∨ is used to denote the logical OR. For example if I have a statement p and a statement q, I can combine them in a disjunction as:

p ∨ q

We already know that the above statement is true as long as at least one of the two statements in either side of ∨ is true.

A Truth Table is used to show the validity of a logical statement for each case (where T stands for true and F stands for false):

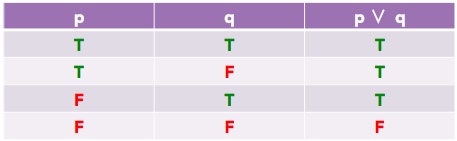
Note that a logical OR is only false when both the left and right statements are false. Makes sense right?

Have I lied if I say "Sunny sky is not rainy or snowy"?

Answer: false (because the statement is true)....

There's something fishy going on with the "or" above. What we really mean to say is "and":

"Sunny sky is not rainy AND sunny sky is not snowy".

Natural language such as English can sometimes be fuzzy that way! But Propositional Logic can never be ambiguous like that. It is always concise.

This is called the Logical AND or sometimes a Conjunction. In Propositional Logic the symbol ∧ is used to denote the logical AND. For example if I have a statement p and a statement q, I can combine them in a conjunction as:

p ∧ q

We already know that the above statement is true as long as both of the two statements in either side of ∧ are true.

Thus here's the Truth Table for the logical AND:

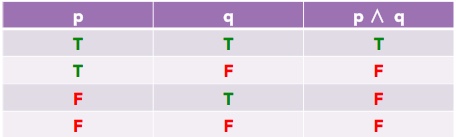Have I lied if I say "Penguins are birds AND only birds can fly"?

Answer: true (the statement to the right of AND is false: balloons can fly too.)....

Question: The above statement is which case in the truth table above?

Answer: 2nd row: The statement to the left of AND (p) is true and the one to the right of AND (q) is false.

Have I lied if I say "It is not the case that penguins can fly"?

Answer: false (the statement is correct!)....

Here we are using what's called Logical NOT or sometimes a Negation. In Propositional Logic the symbol is used to denote the logical NOT. For example if I have a statement p, I can negate it as:

¬p

Obviously, logical NOT flips the validity of a statement. We can give the following Truth Table for it:

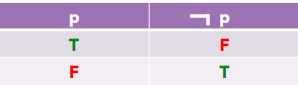Have I lied if I say "If penguins can fly, then sunny sky is green"?

Answer: false (the statement is correct! Although the statement "sunny sky is green" is false, our premise "penguins can fly" is also false. When the premise is false, we are not really telling a lie!)....

This sort of "If ..., then ..." statement is called Logical IF or sometimes an Implication. In Propositional Logic the symbol ⇒ is used to denote the logical implication. For example if I have a statement p which implies a statement q, then I can write:

p ⇒ q

Here's the Truth Table for the logical IF:

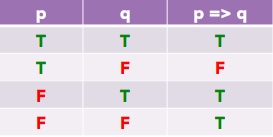
It is interesting to see here is that the only way a logical IF would be telling a lie (false) is when the condition (left-side) is true, and the implication (right-side) is false!

De Morgan's Laws

We can use Truth Tables to decide the validity of more complex statements. For instance, let's construct the table for the logical statement:

¬(p ∧ q)

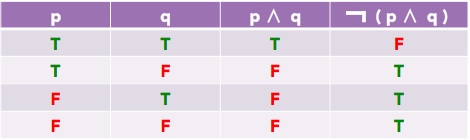
How did we construct this table? That's right. First, I used the table for logical AND to make the 3rd column. Then I used the table for logical NOT to make the 4th column from the 3rd.

Say we now try to construct the table for this statement:

¬p ∨ ¬q

Again, it is easy to make this table. First we use the truth table for NOT to get the 3rd column from the 1st, and to get the 4th column from the 2nd. Then we use the 3rd and 4th columns to fill out the 5th column using the logical OR table:

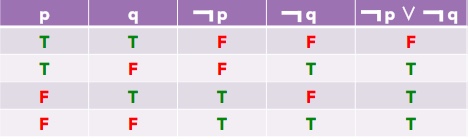
Notice something interesting? The last column in the two tables above is exactly the same!

Whenever this happens, it means the two logical statements are equivalent, that is, they state the same exact fact.

What we just discovered is one of two laws known as the De Morgan Laws:

¬(p ∧ q) = ¬p ∨ ¬q

¬(p ∨ q) = ¬p ∧ ¬q

Exercise: Use truth tables to justify the second law also holds true.